In base all'artefatto che si intende utilizzare, cliccare sul disegno corrispondente allo strumento per accedere alla descrizione dell'attività.

abaco		b.abaco

INTRODUZIONE ABACO  

Durata: circa 2 ore di lezione per ciascuna fase.

Preparazione e Consegna
L’attività ha come obiettivo l’introduzione dell’abaco come strumento di mediazione semiotica rispetto alla costruzione del concetto di notazione posizionale – decimale. Lo strumento (nato dalle attività di commercio di una volta) verrà usato per rappresentare i numeri per contare e calcolare.


Materiali

Nel caso si proponga la costruzione dell’abaco personale:

• 1 base di polistirolo;

• 10 perline monocromatiche o altro materiale (nelle foto: maccheroni). In seguito se ne aggiungeranno altre 9;

• 1 asta (bastoncino per spiedini non ci staranno per ora più di 9 perline, in seguito quando si tratterà di scomporre numeri si valuterà se allungare le aste). In seguito verrà fornito anche il secondo in seguito il terzo;

• scatolina per riporre il materiale;

altrimenti: 

• un abaco di classe.

L’attività è da svolgersi prima a livello individuale, poi a piccolo gruppo ed infine come esposizione collettiva delle riflessioni dei singoli gruppi. 

FASE 1 - Lavoro individuale

Se non si sono ancora fatte considerazioni sul sistema decimale posizionale può essere utile condurre l’attività partendo da questa fase.
Proporre: “Fino ad ora abbiamo lavorato con i numeri da 0 a 10. Sono numeri che riusciamo a rappresentare con le mani. Li abbiamo rappresentati anche con le cannucce e con al linea dei numeri, insieme a numeri più grandi. Tra questi, c’è un numero un po` strano! Secondo te qual è? Cerchialo di blu e spiega perché è strano secondo te. 

0   1   2   3  4   5   6   7   8   9   10 

Prova a scrivere tanti numeri, tutti quelli che conosci. Che cosa noti?”

Si possono dividere i bambini in piccoli gruppi e farli discutere su quanto hanno pensato (se questa è una modalità di lavoro a cui sono abituati). Poi guidare una discussione collettiva guidata. Riportare su quaderno le conclusioni.


FASE 2 - Esplorazione dell’abaco

1) Mostrare ai bambini la scatola contenente i pezzi per costruire un abaco e chiedere:

Secondo voi, a cosa servono queste cose che ho portato? Che cos’è? Com’è fatto? Come si mette insieme? Che cosa fa? Perché lo fa?
L’avete visto usare fuori dalla scuola? Perché la maestra ve lo propone? È simile a qualche altro strumento che avete usato?

È uno strumento di origine antica che serviva per contare e calcolare. Ascoltare tutte le voci dei bambini e far emergere la relazione che questo artefatto può avere con la rappresentazione e composizione dei numeri.

2) Chiedere ai bambini di disegnare con la seguente consegna scritta:

“La maestra ci ha mostrato una scatola. All’interno ci sono…”

FASE 3 - Costruzione di un abaco personale 

Proviamo a costruire un abaco. Ad ogni bambino si consegnano: 

• 1 base di polistirolo;

• 10 perline monocromatiche. In seguito se ne aggiungeranno altre 9;

• 1 asta (bastoncino per spiedini non ci staranno per ora più di 9 perline, in seguito quando si tratterà di scomporre numeri si valuterà se allungare le aste). In seguito verrà fornito anche il secondo in seguito il terzo;

• scatolina per riporre il materiale;

Lavoro di gruppo o individuale

1) Provate a rappresentare i numeri che conoscete con l’abaco”.
2) Cosa accade con il numero 10? Abbiamo visto precedentemente che il 10 è un numero un po’ diverso dagli altri … Disegnate alcune idee su come rappresentare il 10.

Lavoro di classe 

3) Condivisione delle riflessioni fatte in piccolo gruppo o da soli.
4) Condivisione di alcuni schemi d’uso dell’abaco.

Che cosa aspettarsi
I bambini dovrebbero essere a loro agio con i numeri ben oltre il 10, perché proponiamo questa attività alla fine del primo anno o all’inizio del secondo anno di scuola primaria. Per quanto riguarda rappresentare i numeri sull’abaco, è probabile che diversi bambini trovino difficoltà. Per questo la rimandiamo alla fine del primo anno o all’inizio del secondo.
Questo tipo di rappresentazione, infatti, fa fatica ad essere compresa a fondo se non “ha senso” per i bambini. La si può imparare come procedura e basta, ma dopo i dati del primo anno e di altre sperimentazioni preferiamo insegnare procedure con gli altri artefatti, ed in particolare con le cannucce perché mantengono intatto un livello semantico di base forte. Infatti si può parlare di fascetti-decina e di un numero di questi, ma se ne prendo in mano uno vedo e sento ancora 10 cannucce. Invece qui si deve usare una pallina (di quelle che so sono anche messe come unità) e magicamente “vale 10” se viene infilata nella seconda asticella. Questo è davvero difficile perché richiede un passo di astrazione: quello che prima con le cannucce era 1 fascetto-decina (ma vedevo e sentivo ancora il 10) ora è 1 pallina, analoga a quelle delle unità (come le cannucce sciolte che però avevano uno stato molto diverso a livello cinestetico rispetto al fascetto-decina).
Si può vedere un esempio di bimbo con questo tipo di difficoltà in questo video:

Significati matematici che si vogliono costruire 

Si vuole aiutare l’apprendimento della notazione decimale e l’interpretazione dei simboli, rafforzando i legami tra codice arabico, verbale e semantico.

Inoltre può essere una buona occasione per discutere del comportamento dello zero rispetto ad altri numero quando usato per scrivere numeri a più cifre. L’attenzione viene rivolta all’importanza dello zero come segnaposto nella notazione posizionale decimale, che può far cambiare di molto il valore di una cifra all’interno del numero (di quelle alla sua sinistra nel caso dei numeri interi). 

Come costruire i significati matematici 

Durante la prima fase, dovrebbe emergere durante una discussione guidata dall’insegnante che il numero più strano è il 10: per scriverlo si utilizzano due cifre, l’1 e lo 0. Qualcuno potrebbe forse ritenere lo 0 strano perché compare sia nello 0 da solo che nel 10 in seconda posizione. In questo caso si può avviare una discussione intorno allo 0, rispetto a “cosa fa” ad altri numeri quando gli si accompagna. La discussione dovrebbe poi tornare al numero di cifre di cui possono essere composti i numeri. Dalla scrittura di tanti numeri dovrebbe emergere che i numeri dopo il 9 sono combinazioni dei numeri ad una cifra, dallo 0 al 9.
Far scrivere sul quaderno le conclusioni a cui giunge la classe. Per esempio, se non è stato affrontato precedentemente:
“Tra i numero dallo 0 al 10 quello più strano è il 10 perché per scriverlo si utilizzano sia l’1 che lo 0. Scrivendo tanti numeri abbiamo notato che i numeri dopo il nove non sono altro che la combinazione dei numeri da 0 a 9. Per esempio 25, 432, 678 ……. 198765432”. 

È importante che i bambini apprezzino la differenza di significato tra zero da solo, come “assenza di quantità” (“niente”, “nulla”, “nessuna cannuccia o nessun dito alzato)”… e zero come segnaposto quando è vicino a (alla destra di) altre cifre, come nel 10.
Si può poi fornire ai bambini un riquadro riassuntivo, come quello qui sotto, farlo incollare nel quaderno e discuterlo insieme.

 (qui puoi scaricare una copia del quadro riassuntivo)

Con la seconda fase dell’attività ci si dovrebbe mettere in relazione con l’attività delle scatole trasparenti con dentro i fascetti e le cannucce sparse (per es. la fig. sotto). 

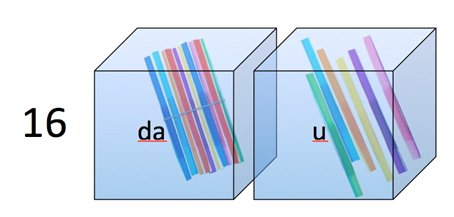
Con le scatole e con l’abaco si aiuteranno i bambini a scoprire che il nostro sistema numerico viene definito decimale posizionale perché il valore delle cifre che compongono un numero è dato dalla loro posizione all’interno del numero stesso.

Dalla terza fase possono emergere riflessioni come: 

• L’ABACO è uno strumento antico che serve per contare e calcolare. 

• Abbiamo provato a capire come utilizzare l’abaco, poi tutti insieme ne abbiamo discusso. Ecco i risultati: si può contare con l’abaco da 0 a 10

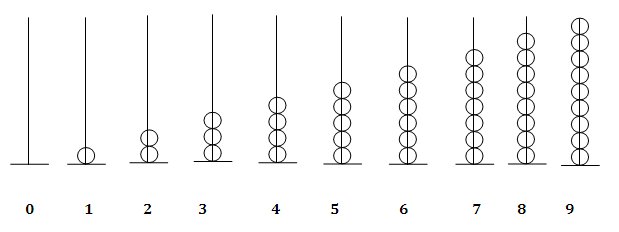
Cosa accade con il 10? La decima pallina non ci sta, l’asta è troppo corta!

Come si fa?

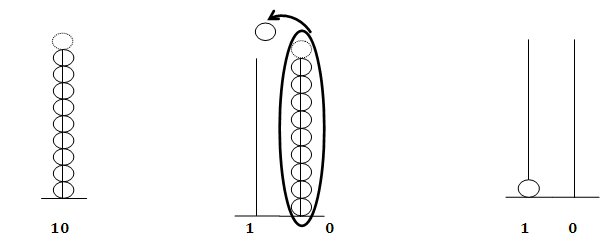
Ho bisogno di un’altra asta e cambio le 10 palline con una pallina che inserisco nella nuova asta a sinistra.

Se emergono difficoltà nella rappresentazione dei numeri sull’abaco, rafforzare la continuità tra la rappresentazione dei numeri con le scatole trasparenti e con l’abaco.

Altre schede-esempio e possibili Compiti
Vengono proposti alcuni esempi per attività su schede, consigliati dopo aver svolto l’ultima fase dell’attività descritta sopra.

Alcuni esercizi suggeriti, a supporto dell’attività, con l’uso di programmi software. 

ABACO E B.ABACO

  Introduzione abaco num. 20

  Lavoriamo con abaco num.  20

  Confronto strumenti num.20

  Confronto strumenti num.100

  Lavoriamo con abaco

  Addizione e sottrazione 2

  Avvio calcolo in colonna