Durata: 2 ore

Preparazione e Consegna

FASE 1
L’insegnante da’ le seguenti consegne:

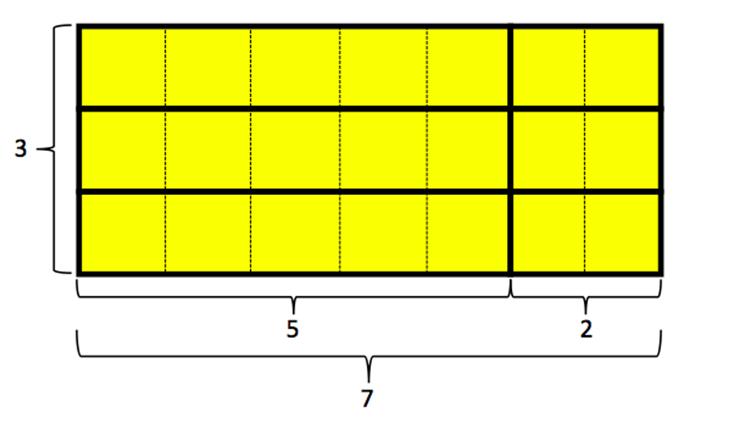
Guardiamo questo diagramma-rettangolo.

L'insegnante disegna alla lavagna la rappresentazione seguente, oppure consegna a tutti i bambini una fotocopia che la contiene.

stampa immagine

e propone ai bambini la scheda di lavoro 1.

FASE 2
L’insegnante da’ le seguenti consegne:

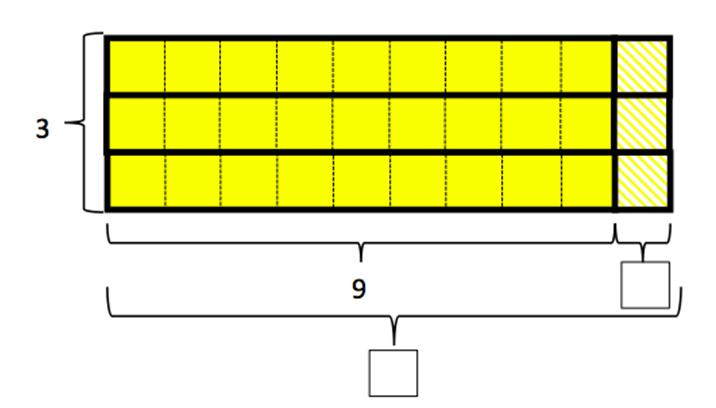
Guardiamo questo diagramma-rettangolo.

L'insegnante disegna alla lavagna la rappresentazione seguente, oppure consegna a tutti i bambini una fotocopia che la contiene.

stampa immagine

e propone ai bambini la scheda di lavoro 2.


Che cosa aspettarsi
I bambini avranno bisogno di un po` di tempo per analizzare le figure e capire che cosa si sta chiedendo loro. Si può richiamare la loro attenzione sui segmenti ingrossati che stanno ad evidenziare parti delle figure. Nella figura proposta nella seconda fase dell’attività compare anche il segno, nuovo rispetto ai diagrammi visti finora, dell’ombreggiatura diversa di una parte “1 per 3 volte” del rettangolo. Si può richiamare a riflettere anche su questo.

Significati matematici che si vogliono costruire
Questa attività mira ad introdurre un modo di visualizzare (ed eventualmente modellizzare mentalmente) l’effetto della scomposizione di numeri nell’addizione ripetuta e nella moltiplicazione. In particolare, se il primo numero (nel caso della prima fase è 7) è visto come composto da due parti (in questo caso 5 e 2) allora quando il numero viene ripetuto, cioè moltiplicato, questa visualizzazione in parti porta a vedere il rettangolo complessivo come composto da due parti (in questo caso “5 per 3 volte” e “2 per 3 volte”, cioè 15 e 6) e questo può agevolare di molto il calcolo a mente. Matematicamente, stiamo introducendo un modo di dare significato a quella che eventualmente (alla scuola secondaria) verrà formalizzata con lettere come proprietà distributiva della moltiplicazione sull’addizione (e sottrazione o somma algebrica).

Come costruire i significati matematici
Prima di far parlare i bambini tra loro può essere utile lasciare a tutti il tempo di riflettere ed interpretare la (almeno la prima) consegna. Così la discussione collettiva successiva potrà essere arricchita da più voci con interpretazioni diverse.
Non servirà mai usare la terminologia “proprietà distributiva”, ma consigliamo di far discutere a lungo i bambini sulle loro conclusioni in merito all’interpretazione dei due diagrammi-rettangolo con le evidenziazioni.
Nelle rappresentazioni abbiamo richiamato ancora l’uso delle (solite) parentesi graffe per suggerire ai bambini di vedere i numeri come complementari tra loro, in base a come sono disposte le parentesi.
Durante questa sequenza di tre attività i diagrammi-rettangolo dovrebbero diventare uno strumento per esplicitare come ciascun bambino sta pensando ad un determinato calcolo. Consigliamo di continuare a lavorare con queste rappresentazioni a lungo e di richiamarle spesso durante l’anno per agevolarne l’interiorizzazione, in modo che possano diventare strumento efficace per il calcolo a mente.
In alcune classi i bambini hanno cominciato a parlare di “quadratini fantasma” nel caso in cui si sceglie una scomposizione come 9 in 10-1, o in generale come n in a-b (dove b+n=a).

	In questo filmato Anna (non è l'insegnante della classe) presenta una rappresentazione dei diagramma-rettangolo 7 per 3 volte e promuove una condivisione di strategie proposte dai bamb9ni per calcolare il totale dei quadretti, senza contarli uno per uno. I bambini propongono diverse strategie, che in gran parte non fanno uso della scomposizione proposta. E' un caso in cui si vede chiaramente come una notazione che può essere significativa per l'insegnante o esperti coinvolti, non lo è necessariamente per i bambini.
	La domanda iniziale viene rilanciata dall'insegnante Roberta, che cerca di riportare l'attenzione dei bambini sulla scomposizione proposta del 7, in 5 e 2. Si vede chiaro il tentativo di Anna e Roberta di portare l'attenzione dei bambini sui pezzi 5 per 3 volte e 2 per 3 volte, selezionando affermazioni dei ragionamenti proposti dai bambini.  Una volta descritta una strategia per la scomposizione proposta, la maestra rappresenta una scomposizione diversa ( 7= 3 + 4, poi 7 = 3 +2 + 2) proposta da Sara.
	In questo filmato un bambino cerca di calcolare 8x6 rappresentando la situazione con i diagrammi rettangolo. Spiega come ha scomposto l’8 e come calcola le varie parti del diagramma ottenuto, per poi rimetterle insieme nell’addizione finale.
	In questo filmato Bea sta calcolando 8x6. Spiega come ha pensato a 8 come 10-2, immaginando dei “quadretti fantasma”, con cui si aiuta per rappresentare ed eseguire il calcolo.

Altre schede-esempio e possibili Compiti

Proponiamo di dare altri esercizi di rinforzo simili, e di far inventare ai bambini rettangoli che rappresentino particolari prodotti (meglio se sconosciuti).