|
|
RAPPRESENTAZIONI
NUMERI CON MANI
Prerequisiti: costruzione linea a
finestra scorrevole e contamani
Durata: 2 ore.
Materiale
• contamani personale;
• contamani di classe;
• linea di numeri di classe;
• LIM o computer per la fase 3, se affrontata.
Preparazione e Consegna
Durante questa attività si andrà verso un modo privilegiato di
rappresentare i numeri con le mani e il contamani. Questo modo sarà
utile per strategie di calcolo a mente come la Composizione
e scomposizione del 5 e del 10.
FASE 1
1) Chiedere ai bambini di rappresentare
vari numeri compresi tra 5 e 10, usando le seguenti modalità:
a) dicendo un numero a voce (per
esempio “sette”)
b) mostrando un numero sulla linea dei numeri di classe,
evidenziandolo con la finestra scorrevole.
Ciascun bambino da posto
deve posizionare il proprio contamani in modo da rappresentare il numero
scelto dall’insegnante (a turno si possono anche chiamare fuori dei
bambini che “diano i numeri”.
Chiedere poi ai bambini di rappresentare il numero con il contamani più
velocemente possibile.
FASE 2
Usare quest’attività per
riflettere su:
Qual è il modo più
veloce di rappresentare questi numeri con i contamani?
Far riflettere i bambini
sulle strategie che hanno usato.
Arrivare all’istituzionalizzazione seguente:
Quindi possiamo pensare ai
numeri così:

e facilmente rappresentarli sulle dita così:

Nota: Per le mani c’è una variazione
sul n. 4, dove, invece di scegliere l’accrescimento che costringerebbe
una piegatura innaturale delle dita, si può scegliere di spostare il
numero sulle dita lunghe e lasciare fuori il pollice, onde facilitare la
manualità, ma va bene rappresentare il 4 anche nell’altro modo.
Consigliamo di fare attenzione alle dita alzate e abbassate per ciascun
numero.
FASE 3
Proporre il gioco in laboratorio di informatica o alla LIM: “Indovinelli
con le dita”.
Che cosa aspettarsi
I bambini dovrebbero essere a loro agio a rappresentare numeri con le
mani e con il contamani. Probabilmente non avranno ancora interiorizzato
particolari configurazioni preferenziali per alcuni numeri (per esempio
7 come 5 e 2 o 6 come 5 e 1), che con questa attività dovrebbero
cominciare a sviluppare. Alcuni bambini forse useranno inconsapevolmente
alcune delle rappresentazioni preferenziali e si possono usare le
rappresentazioni di questi bambini per introdurle.
Significati matematici che si vogliono costruire
Si vogliono potenziare aspetti semantici dei numeri, in particolare
rappresentazioni analogiche. Studi neuroscientifici dimostrano che una
maggior consapevolezza delle dita è correlato con abilità numeriche più
sviluppate. Dunque, usare le mani e rappresentazioni delle (proprie)
mani, dovrebbe potenziare la consapevolezza delle proprie mani e dita,
la cosiddetta gnosia digitale.
Inoltre con queste attività si intende sottolineare, in maniera
istituzionale, la preferenza di particolari modalità di
rappresentazione analogica dei numeri, che risultano particolarmente
comode per efficaci strategie di calcolo a mente (passaggio e ritorno al
5 e al 10). Facendo attenzione anche alle dita abbassate, si potenzia la
conoscenza dei numeri complementari rispetto al 10.
Infine si potenziano abilità metacognitive di riflessione sulle
strategie usate.
| Contare intransitivo |
|
| Contare transitivo |
|
| Aspetto ordinale del
numero |
si |
| Aspetto cardinale del
numero |
si |
| Rappresentazioni del
numero |
simbolico scritto e
orale, analogico |
| Confronto fra numeri |
si |
| Abbinamento quantità/numero |
si |
| Problemi additivi
(addizione-sottrazione) |
si |
| Spazio e figure |
|
| Artefatti/strumenti |
contamani, linea dei
numeri |
Come costruire i significati matematici
Durante la seconda fase discutere insieme per arrivare alla conclusione
che è utile lasciare alzate tutte le dita di una mano, cioè 5, per poi
aggiustare soltanto le dita dell’altra mano. In questo modo i numeri
vengono scomposti, per esempio, così: il 7 in 5 e 2, il 6 in 5 e 1, il
9 in 5 e 4 eccetera. Se il 10 è riconosciuto come configurazione
“base” con le dita tutte su, potrebbero emergere anche strategie
come: 8 è 5 e 5 abbasso 2, il 9 è 5 e 5 abbasso 1.
Per la discussione delle strategie usate si può chiamare un bambino per
mostrare quello che ha fatto sul contamani grande di classe.
Far scrivere le considerazioni riassuntive e conclusive sul quaderno.
Per esempio, si potrebbe arrivare ad un riassunto conclusivo di questo
tipo:
Eventualmente
i bambini potranno notare che la “e” non è nient’altro che
“+”, un’addizione.
Dopo aver lavorato con “l’abbassamento” delle dita il riassunto
potrebbe assomigliare a questo:
Di solito partiamo
con il contamani azzerato. E se invece il contamani avesse
tutte le dita alzate?
Per
essere veloci con il contamani:
1
 5 ABBASSO 4 E ABBASSO
5
5 ABBASSO 4 E ABBASSO
5
2 5 ABBASSO 3 E ABBASSO
5
5 ABBASSO 3 E ABBASSO
5
3 5 ABBASSO 2 E ABBASSO
5
5 ABBASSO 2 E ABBASSO
5
4 5 ABBASSO 1 E ABBASSO
5
5 ABBASSO 1 E ABBASSO
5
5
 5 E 5 ABBASSO
5 oppure
10 ABBASSO 5
5 E 5 ABBASSO
5 oppure
10 ABBASSO 5
6 5 E 5 ABBASSO
4 oppure
10 ABBASSO 4
5 E 5 ABBASSO
4 oppure
10 ABBASSO 4
7 5 E 5 ABBASSO
3 oppure
10 ABBASSO 3
5 E 5 ABBASSO
3 oppure
10 ABBASSO 3
8 5 E 5 ABBASSO
2 oppure
10 ABBASSO 2
5 E 5 ABBASSO
2 oppure
10 ABBASSO 2
9 5 E 5 ABBASSO
1 oppure
10 ABBASSO 1
5 E 5 ABBASSO
1 oppure
10 ABBASSO 1
10 5 E 5
oppure 10
5 E 5
oppure 10
|
Eventualmente
i bambini potranno essere guidati a notare che ABBASSO sta per “-“,
sottrazione.
Attenzione: Qui si sta proponendo
una variazione significativa rispetto a quanto evidenziato in
precedenza, che dovrebbe corrisponde ad un’evoluzione cognitiva. Per
esempio, con il memory delle mani l’attenzione era sull’indifferenza
delle dita scelte purché il numero totale sollevato corrispondesse al
numero da rappresentare (e questo va bene in una prima fase). Ora si sta
facendo esplicitare ai bambini quella che loro dovrebbero aver costruito
e conquistato come nuovo modo di pensare, più evoluto: ora quali dita
si alzano è importante per economia di pensiero.
Non è sbagliato quello che i bambini facevano prima e può darsi che
alcuni vorranno usare modi di pensare meno evoluti, ma aiutando chi ha
costruito nuovi modi di pensare più economici ad esplicitarli può
essere utile per il resto della classe. L’aspetto metacognitivo di
questo tipo di attività è fondamentale e importante da curare durante
tutto l’anno scolastico.
Compiti e Altre Proposte
Quando è possibile, in forma di gioco, per esempio mentre i bambini si
mettono in fila, o durante la ricreazione, o mentre si aspetta in
mensa…proporre le seguenti attività:
1) L’insegnante dice: “Fatemi veder 9” e i bambini devono alzare
le dita corrispondenti
2) L’insegnante dice: “Che numero è?” (alzando 5 dita aperte e
ancora 1 dell’altra mano)
3) Nascondendo dietro la schiena le mani, l’insegnante dice:
“Immaginate di vedere le mie mani dietro la schiena. Ho tutte le dita
di una mano sollevate e due dita dell’altra mano abbassate. Che numero
è?” (si veda anche l’attività Giochi
con mani e contamani).
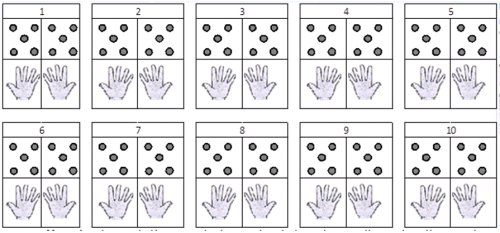
4) Mostrare configurazioni “simmetriche” come quelle nelle figure
sotto e chiedere ai bambini che numeri rappresentano. Arrivare a notare
che 2 e 4 rappresenta lo stesso numero che 4 e 2 [non occorre
appiccicare le etichette “simmetrico” o “commutativo”, ma far
esplicitare ai bambini quello che notano.].

Copia della scheda
è presente è scaricabile cliccando qui.
5) Proporre varie "addizioni con le
dita", simile alla scheda allegata.
6) Proporre esercizi di completamento della decina.
7) Per esercitare i bimbi sulla complementarietà con processi inversi
rispetto al calcolo di una somma, si suggerisce l'uso del programma Dadi
e Obbiettivo
numero:
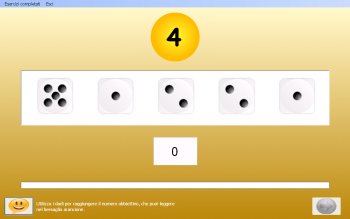

Esempi di schede per l'attività e i compiti sono elencati nei Materiali
allegati.
Altri esercizi
suggeriti, a supporto dell’attività, con l’uso di programmi
software.
Inizio
pagina
|
LINEA
DEI NUMERI
 Appello
con cannucce
Appello
con cannucce
 Costruzione
Linea 1-10
Costruzione
Linea 1-10
 Costruzione
linea 1-20 Costruzione
linea 1-20
 Costruzione
linea finestra scorrevole Costruzione
linea finestra scorrevole
 Linea
numeri a finestra scorrevole Linea
numeri a finestra scorrevole
 Introduzione
10 con Linea numeri Introduzione
10 con Linea numeri
 Confrontare
numeri Confrontare
numeri
 Rappresentazioni
numeri con mani Rappresentazioni
numeri con mani
 Maggiore e Minore su Linea numeri
Maggiore e Minore su Linea numeri
 Avanti e indietro su Linea numeri
Avanti e indietro su Linea numeri
 Numeri pari e dispari
Numeri pari e dispari
 Materiali
Materiali
|






