|
|
NUMERI PARI E DISPARI
Durata: Un’ora di lezione, ma
suggeriamo di ripetere gli esercizi proposti nell’attività, fino a
che le nozioni siano state appropriate dai bambini.
Preparazione e Consegna
L'insegnante disporrà per terra la linea dei numeri di classe e metterà
a disposizione dei bambini un centinaio di cannucce, delle forbici e del
nastro adesivo.
Materiali
- 100 cannucce circa;
- linea dei numeri grande di classe, a tacche;
- nastro adesivo trasparente;
- forbici.
FASE 1
Chiedere ai bambini di rappresentare il percorso dall’inizio della
linea (punto di partenza, o “0”) al numero 20 (o numero massimo
rappresentato sulla linea) con una cannuccia per ogni tratto (una sul
segmento 01, una sul segmento 02, ecc, e le cannucce di tratti
successivi sono adiacenti). Le cannucce vanno attaccate su ogni segmento
della linea con il nastro adesivo. Se necessario tagliare le cannucce.
Questo può anche essere predisposto prima dall’insegnante.
Si chiede ai bambini di riflettere sulle seguenti domande mirando allo
sviluppo della loro consapevolezza del numero di cannucce comprese tra i
numeri di riferimento ad ogni domanda.:
“Adesso cosa potete dire sul percorso dal punto di partenza (o
“zero”) al 7?”
“…e fino al numero 10? e 12? e 20?”
“Che cosa potete dire sul percorso dal 5 al 10? E dal 5 al 7?”
“…e dal 10 al 3?”
FASE 2
Ora tagliare a metà circa 50 cannucce (se sono troppo lunghe,
altrimenti usarle intere) e cominciare a disporle sotto a ciascun numero
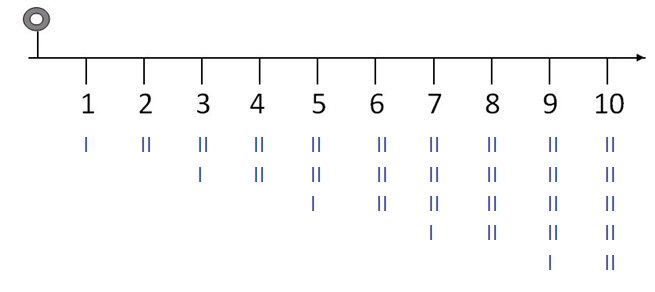
della linea nel modo seguente:
- sotto all’1 una cannuccia
- sotto al 2 due cannucce affiancate,
- sotto al 3 due cannucce affiancate, alla stessa altezza della
coppia sotto il 2, e una singola sotto,
- sotto al 4 due coppie di cannucce, la prima coppi all’altezza
della coppia sotto al 2,
- sotto al 5 due coppie di cannucce come per il 4 e poi una singola
sotto.
Chiedere ai bambini:
“Come continuereste a disporre cannucce se doveste proseguire voi
fino al 10 (o 20)?”
Poi continuare a riflettere su proprietà dei numeri evidenziati in
questo modo. Per esempio:
“Proviamo ora a passare dall’1 al 3 al 5. Che cosa succede
proseguendo lungo la linea (in termini di cannucce percorse e di
cannucce che si vedono sotto a ciascun numero)?”
“Proviamo ora a passare dal 2 al 4 al 6. Che cosa succede
proseguendo lungo la linea (in termini di cannucce percorse e di
cannucce che si vedono sotto a ciascun numero)?”
“Per passare dal 12 al 14 che cosa succede? e dal 12 al 13?”
“Se dico di metterti sul numero che ha 3 coppie di cannucce dove
vai?”
“Se dico di andare sul numero che ha 4 coppie di cannucce e una
singola dove vai?”
Che cosa aspettarsi
Durante la prima fase, è probabile che i bambini riescano velocemente a
prestare attenzione alle cannucce contenute tra i due numeri di
riferimento di volta in volta, perché hanno fatto considerazioni simili
anche prima di aver disposto cannucce sui tratti della linea.
Invece nella seconda fase ci potrebbe essere più difficoltà ad
esplicitare le regolarità tra le rappresentazioni dei diversi tipi di
numeri; in questo caso la differenza significativa è tra “pari”,
cioè numeri che si possono rappresentare con “coppie” di
cannucce” e dispari, cioè numeri che si possono rappresentare con
“coppie di cannucce più una”. Forse bisognerà aiutare i bambini a
considerare queste regolarità.
Significati matematici che si vogliono costruire
Con questa attività si lavora sulla proprietà dei numeri naturali di o
pari o dispari (e non entrambe le cose), cioè si impara a notare che
alcuni numeri possono essere rappresentati come multipli di 2 mentre
altri no, perché avanza sempre uno.
Come costruire i significati matematici
È utile far emergere una terminologia rispetto alla “coppia” di
cannucce da sostituirsi eventualmente con “multiplo di due” o “due
per qualcosa”. Quindi numeri come 2, 4, 6, … si possono leggere come
“tot coppie di cannucce” oppure come “2 per tot volte”, mentre i
numeri come 1, 3, 5,… si possono leggere come “tot coppie più una
cannuccia”, o “2 per tot volte più uno”. È importante che i
bambini sviluppino scioltezza nel saper come passare da un pari (o
dispari) al pari (o dispari) successivo, o anche a saltare più di un
pari (o dispari) alla volta, esplicitando come si sommano o sottraggono
gruppetti di cannucce ad ogni passaggio. In particolare, andare avanti e
indietro sui pari (o sui dispari) implica aggiungere o togliere sempre
multipli di due alla volta.
| Contare intransitivo |
|
| Contare transitivo |
si |
| Aspetto ordinale del
numero |
si |
| Aspetto cardinale del
numero |
si |
| Rappresentazioni del
numero |
simbolico e analogico |
| Confronto fra numeri |
si |
| Abbinamento quantità/numero |
si |
| Problemi additivi
(addizione-sottrazione) |
si |
| Spazio e figure |
|
| Artefatti/strumenti |
cannucce, linea dei
numeri |
In
allegato, nei Materiali, sono presenti schede di supporto
all'attività.
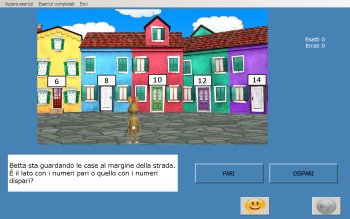
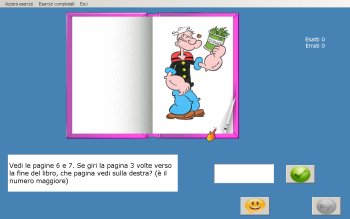
Si suggerisce l'uso del programma
software "Pari e Dispari" la cui realizzazione è in corso
di ultimazione.
Inizio pagina
|
LINEA
DEI NUMERI
Appello
con cannucce
Costruzione
Linea 1-10
Costruzione
linea 1-20
Costruzione
linea finestra scorrevole
Linea
numeri a finestra scorrevole
Introduzione
10 con Linea numeri
Confrontare
numeri
Rappresentazioni
numeri con mani
Maggiore e Minore su Linea numeri
Avanti e indietro su Linea numeri
Numeri
pari e
dispari
Materiali
|