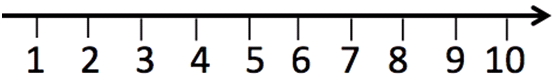|
|
INTRODUZIONE
10 CON LINEA DEI NUMERI
Materiali
- Cartellini con scritti i numeri
introdotto fino al 10 (incluso)
- 10 (o 11) bicchieri di plastica
- 55 cannucce
- un elastico
- linea dei numeri
Presentare delle tesserine con scritti in
maniera simbolica i numeri da uno (o zero nelle classi in cui è stato
introdotto) a dieci e proporre:
“Per ogni tesserino prendete un bicchiere e metteteci il numero
corrispondente di cannucce.”
Poi
“Vi
ricordate come abbiamo messo in ordine i numeri il giorno …
(riferirsi all’attività di ordinamento se affrontato
precedentemente, per esempio ordinando i cani dalmata o in attività
di ordinamento numerosità come “indovina la scatola” magari
riproposti mentre venivano introdotti i numeri - Le attività sono
descritte in Prime attività di classe).
Ora
mettiamo in ordine tutti questi numeri.”
Farsi aiutare dalla classe intera o da un bambino nella disposizione
ordinata delle tesserine e dei bicchieri corrispondenti.
“Che cosa notate?” Promuovere una breve discussione matematica.
“Facciamo un disegno sul quaderno di quello che abbiamo fatto
adesso.”
Le
pagine con i numeri da stampare, possibilmente su cartoncino, e
ritagliare sono scaricabili cliccando qui.
Significati matematici che si vogliono costruire
Si vuole arrivare ora all’introduzione della linea dei numeri come
successione di numeri che rappresentano quantità sempre maggiori con le
seguenti caratteristiche:
-
ogni
numero rappresenta una quantità maggiore di quello che lo precede e
minore di quello che lo segue;
-
ogni
numero rappresenta una quantità che è esattamente 1 più del
numero che lo precede;
-
c’è
un numero che è più piccolo di tutti (lo 0 in classi in cui è
stato introdotto o l’1 in classi in cui non è stato introdotto lo
0).
Come costruire i significati matematici di riferimento
È importante ancora riferirsi anche alle rappresentazioni analogiche
dei numeri ottenute mediante le cannucce nei bicchieri. Quando si arriva
a rappresentare il dieci con le cannucce è bene rafforzare
l’abitudine di legare le cannucce in un fascetto per ricordare il
concetto di decina, associandolo alla rappresentazione simbolica del
numero.
Con la domanda: “Che cosa notate?” si vogliono far emergere le
caratteristiche riportare sopra e cioè che
-
ogni
numero rappresenta una quantità maggiore di quello che lo precede e
minore di quello che lo segue;
-
ogni
numero rappresenta una quantità che è esattamente 1 più del
numero che lo precede;
-
c’è
un numero che è più piccolo di tutti (lo 0 in classi in cui è
stato introdotto, o l’1 in classi in cui non è stato introdotto
lo 0).
I
bambini faranno molti altri commenti, che l’insegnante può riportare
alla lavagna o su un cartellone. Tuttavia il confronto di idee va
portato verso le osservazioni descritte sopra.
La
formalizzazione sul quaderno prevede la scrittura di una linea dei
numeri come questa:
a) in classi in cui si sceglie
di non introdurre lo zero sulla linea (consigliato dal progetto):
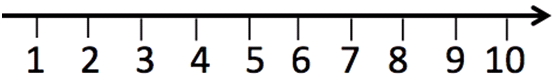
con
eventualmente le quantità analogiche rappresentate sotto a ciascun
numero; in cui ci sono difficoltà sulla semantica dello 0:
oppure
b)
in classi in cui si sceglie di introdurre lo zero sulla linea
consigliamo una rappresentazione così:

ma consigliamo comunque di non insistere troppo sul significato di
zero soltanto come “quantità nulla” o “niente”.
Per la costruzione della linea dei numeri 1-10 e modelli di linea già
preparati, vedi Costruzione linea numeri 1- 10.
Cogliamo ora l’occasione per esporre la nostra posizione sul
trattamento dello zero sulla linea dei numeri all’inizio del percorso
scolastico. Le riflessioni sono riprese dalla pubblicazione
“Trattamento dello Zero nel Progetto PerContare” (Baccaglini-Frank,
2013).
| .........
Complessità cognitiva dello
zero
Come si può leggere nel primo capitolo del Handbook of
Mathematical Cognition (2005), dati da studi sullo sviluppo
(Hughes, 1986) indicano che imparare la sequenza di numeri (1
– 9) sia in generale non-problematico. Lo zero invece sembra
causare più difficoltà (Wellman & Miller, 1986), ma non
sono ancora del tutto chiare le ragioni. Dagli studi emerge che
solo per leggere lo zero, come cifra, all’interno di numeri
sono richiesti negli adulti tempi eccezionalmente lunghi (Brysbaert,
1995); inoltre, nella scrittura di numeri a più cifre, lo zero
causa particolari difficoltà. Per i bambini queste difficoltà
portano ad errori nella scrittura dei numeri che hanno zeri
interposti tra altre cifre, e quando devono scrivere “0” i
bambini spesso eseguono movimenti differenti rispetto a quando
scrivono le altre cifre (Lochy, Pillon Zesiger, & Seron,
2002). Le difficoltà più significative nella gestione delle
cifre arabe e dello 0 in particolare riguardano l’uso della
notazione posizionale e, in particolare, il fatto che il valore
di una cifra cambi in base alla posizione che occupa
all’interno di un numero (p.e. 1 può valere un’unità, ma
anche una decina, un centinaio, ecc.). Anche in pazienti con
lesioni cerebrali, lo zero è oggetto di errori selettivi
rispetto al ruolo sintattico o lessicale che assume nel numero (Granà,
Lochy, Girelli, Seron, & Semenza, 2003). Il fatto, poi, che
lo zero come numero significhi la “non presenza”
dell’oggetto di riferimento, e quindi una “non-quantità”
può essere fonte di ulteriori difficoltà a livello semantico.
Dunque è assodato che la gestione dello zero sia cognitivamente
più complessa che la gestione degli altri numeri e che questo
possa portare ad una serie di difficoltà nel suo uso nella
lettura e nella scrittura del codice arabo (Dehaene, 1992).
Vediamo ora, rispetto ai contenuti aritmetici delle prime classi
della scuola primaria, quali aspetti dello zero siano da
prendere in considerazione.
Ricordiamo qui che il progetto PerContare propone delle pratiche
di “buona didattica” della matematica (Baccaglini-Frank e
Robotti, 2013; Baccaglini-Frank e Scorza, 2013) per la classe
intera, facendo particolare attenzione ai bambini con difficoltà
d’apprendimento, ma senza dimenticare gli altri bambini, anche
quelli con prestazioni alte. Questo è un bisogno quanto mai
impellente in un contesto come quello italiano in cui le classi
accolgono bambini con caratteristiche cognitive e bisogni
educativi differenti tra loro. Per questo, da un lato le attività
proposte nel progetto sono particolarmente attente ad evitare
fattori che possono aumentare le difficoltà individuali di
apprendimento, e dall’altro hanno come obiettivo didattico
quello di aiutare tutti i bambini della classe a costruire
solidi significati matematici, secondo le normative
ministeriali. Dunque vengono avanzate proposte che potrebbero
essere utilizzate, con piccoli adattamenti, anche in un lavoro
individuale di potenziamento (Biancardi, Lucangeli, 2010;
Biancardi et al., 2011; Lucangeli, 2012), ma che generalmente
sono concepite per la classe intera, consentendo a tutti i
bambini di affrontare situazioni cognitivamente appaganti e
fonte di “nuovo Sapere” (Bartolini Bussi e Mariotti, 2009).
Tipicamente cerchiamo di costruire le attività in modo che
abbiano una “soglia bassa” e un “soffitto alto” perché
tutti i bambini possano trovare modo di essere ingaggiati e
perché ciascuno possa vincere delle piccole sfide cognitive,
lavorando nella sua zona di sviluppo prossimale (Vygotsky,
1987).
Rispetto all’introduzione dello zero, questo significa che le
attività eviteranno inutili appesantimenti cognitivi che
possono sfociare in errori nei bambini più in difficoltà, ma
non trascureranno la delicata questione dello zero:
affronteranno, in maniera graduale, la sua introduzione come
segno (“0”) con un particolare significato prima come
semplice segnaposto nella addizione e sottrazione (anche
informali) sulla linea dei numeri, e poi come quantità nulla o
“non-considerazione di oggetti che prima erano stati
considerati” (p.e., “nessun dito alzato”, o “nessun
oggetto rimasto”)....
.... .
leggi la pubblicazione completa
|
Preparazione e compiti
Oltre alle attività descritte possono essere utilizzate le schede in Materiali.
Alcuni
esercizi suggeriti, a supporto dell’attività, con l’uso di programmi
software.
| Contare intransitivo |
è possibile |
| Contare transitivo |
si |
| Aspetto ordinale del
numero |
|
| Aspetto cardinale del
numero |
si |
| Rappresentazioni del
numero |
orale e scritto |
| Confronto fra numeri |
si |
| Abbinamento quantità/numero |
si |
| Problemi additivi
(addizione-sottrazione) |
|
| Spazio e figure |
|
| Artefatti/strumenti |
cannucce |
Inizio
pagina
|
LINEA
DEI NUMERI
 Appello
con cannucce
Appello
con cannucce
 Costruzione
Linea 1-10
Costruzione
Linea 1-10
 Costruzione
linea 1-20 Costruzione
linea 1-20
 Costruzione
linea finestra scorrevole Costruzione
linea finestra scorrevole
 Linea
numeri a finestra scorrevole Linea
numeri a finestra scorrevole
 Introduzione
10 con Linea numeri Introduzione
10 con Linea numeri
 Confrontare
numeri Confrontare
numeri
 Rappresentazioni
numeri con mani Rappresentazioni
numeri con mani
 Maggiore e Minore su Linea numeri
Maggiore e Minore su Linea numeri
 Avanti e indietro su Linea numeri
Avanti e indietro su Linea numeri
 Numeri pari e dispari
Numeri pari e dispari
 Materiali
Materiali
|